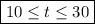Question

During a fireworks show, a rocket is fired vertically upward with an initial velocity of 200 meters per second. The height in meters, s, of the rocket in t seconds may be approximated by s = 200t – 5t2. The rocket must be at least 1,500 meters in the air to safely explode. In which time interval may it safely be exploded 30 ≤ t ≤ 40 seconds 0 ≤ t ≤ 10 seconds 10 ≤ t ≤ 40 seconds 10 ≤ t ≤ 30 seconds

Answer 1

`10\leq t\leq 30`

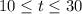
Explanation:

Inequalities

The height s (in meters) of a rocket fired vertically in t seconds may be approximated by

`s = 200t-5t^2`

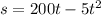
The rocket needs to reach a minimum height of 1,500 m, thus

`200t-5t^2\geq 1,500`

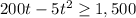
Simplifying by 5

`40t-t^2\geq 300`

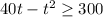
Rearranging (recall the direction of the inequality changes when multiplying by negative numbers)

`t^2-40t+300\leq 0`

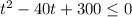
Factoring

`(t-10)(t-30)\leq 0`

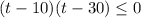
The solution of this inequality is t ranging from 10 to 30, thus

`\boxed{10\leq t\leq 30}`