Answer:
see the explanation
The graph in the attached figure
Explanation:
we have
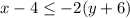
isolate the variable y
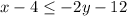
Adds 12 both sides
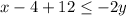
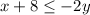
Divide by -2 both sides
Remember that when you multiply or divide both sides of an inequality by a negative number, you must reverse the inequality symbol
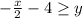
Rewrite
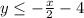
we know that
The solution of the inequality is the shaded area below the solid line
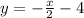
The slope of the solid line is negative m=-1/2
The y-intercept of the solid line is (0,-4)
The x-intercept of the solid line is (-8,0)
therefore
The graph in the attached figure
A solution of the inequality could be (0,-4)
because the point (0,-4) lie in the shaded area of the solution set