Question

Which of the tables below could represent a linear function?

1. x: 0, 2, 4
f(x): -11, -13, -10
2. x: 1, 2, 3
f(x): 33, 11, 49
3. x: 0, 10, 20
f(x): 8, 18, 28
4. x: 0, 5, 10
f(x): -20, -25, -30

Answer 1

1. Is not linear 2. Is not linear 3. Is linear 4. Is linear

Explanation:

A function is said to be linear if it is in the form y = mx + c, where x and y represent its ordered pair (x,y) and m is the gradient and c its y- intercept. For function to be linear, for any three consecutive points (x₁,y₁), (x₂,y₂) and (x₃,y₃) the gradient, m will be constant. This follows that
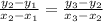`(y_(2) -y_(1) )/(x_(2) - x_(1) ) = (y_(3) -y_(2) )/(x_(3) - x_(2) )` for these points. We now insert the 3 points in each pair of data in the order x₁, x₂, x₃ and the corresponding y = f(x) as y₁, y₂, y₃ respectively.

For set 1

x₁ = 0, x₂ = 2, x₃ = 4, y₁= f(x₁) = -11, y₂ = f(x₂)= -13, y₃ = f(x₃) = -10.

So,
`([-13-(-11)])/(2-0) = -1 L.H.S\\ ([-10-(-13)] )/(4-2) = (3)/(2) R.H.S`

Since -1 ≠
`(3)/(2)`

The function is not linear.

For set 2

x₁ = 1, x₂ = 2, x₃ = 3, y₁= f(x₁) = 33, y₂ = f(x₂)= 11, y₃ = f(x₃) = 49.

So,
`([11-33)])/(2-1) = -22 L.H.S\\ ([49-11)] )/(3-2) = 38 R.H.S`

Since -22 ≠ 38

The function is not linear.

For set 3

x₁ = 0, x₂ = 10, x₃ = 20, y₁= f(x₁) = 8, y₂ = f(x₂)= 18, y₃ = f(x₃) = 28.

So,
`([18-8)])/(10-0) = 1 L.H.S\\ ([28-18)] )/(20-10) = 1 R.H.S`

Since 1 (L.H.S) = 1 (R.H.S)

The function is linear.

For set 4

x₁ = 0, x₂ = 5, x₃ = 10, y₁= f(x₁) = -20, y₂ = f(x₂)= -25, y₃ = f(x₃) = -30.

So,
`([-25-(-20)])/(5-0) = -1 L.H.S\\ ([-30 -(-25)])/(10-5) = -1 R.H.S`

Since -1 (L.H.S) = -1 (R.H.S)

The function is linear.