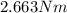Question

A metal has a strength of 414 MPa at its elastic limit and the strain at that point is 0.002. Assume the test specimen is 12.8-mm dia and has a 50-mm gage length. What is its modulus of elasticity? What is the strain energy at the elastic limit? Can you define the type of metal based on the given data?

Answer 1

To solve this problem, we will start by defining each of the variables given and proceed to find the modulus of elasticity of the object. We will calculate the deformation per unit of elastic volume and finally we will calculate the net energy of the system. Let's start defining the variables

Yield Strength of the metal specimen

`S_(el) = 414Mpa`

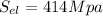
Yield Strain of the Specimen

`\epsilon_(el) = 0.002`

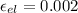
Diameter of the test-specimen

`d_0 = 12.8mm`

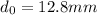
Gage length of the Specimen

`L_0 = 50mm`

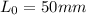
Modulus of elasticity

`E = (S_(el))/(\epsilon_(el))`

`E = (414Mpa)/(0.002)`

`E = 207Gpa`

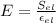
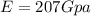
Strain energy per unit volume at the elastic limit is

`U'_(el) = (1)/(2) S_(el) \cdot \epsilon_(el)`

`U'_(el) = (1)/(2) (414)(0.002)`

`U'_(el) = 414kN\cdot m/m^3`

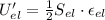
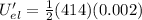
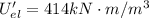
Considering that the net strain energy of the sample is

`U_(el) = U_(el)' \cdot (\text{Volume of sample})`

`U_(el) = U_(el)'((\pi d_0^2)/(4))(L_0)`

`U_(el) = (414)((\pi*0.0128^2)/(4)) (50*10^(-3))`

`U_(el) = 2.663N\cdot m`

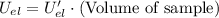
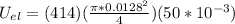
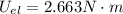
Therefore the net strain energy of the sample is
`2.663N\codt m`