Question

PLEASE HELP

Use the function f(x) to answer the questions.

f(x) = −16x2 + 22x + 3

Part A: What are the x-intercepts of the graph of f(x)? Show your work. (2 points)

Part B: Is the vertex of the graph of f(x) going to be a maximum or a minimum? What are the coordinates of the vertex? Justify your answers and show your work. (3 points)

Part C: What are the steps you would use to graph f(x)? Justify that you can use the answers obtained in Part A and Part B to draw the graph. (5 points)

Answer 1

First graph

• y=-16x^2+22x+3(Graph attached)

#A

Use quadratic formula

`\\ \rm\rightarrowtail x=(-b\pm√(b^2-4ac))/(2a)`

`\\ \rm\rightarrowtail x=(-22\pm√(484+192))/(-32)`

`\\ \rm\rightarrowtail x=(-22\pm√(676))/(-32)]/tex]</p><p>[tex]\\ \rm\rightarrowtail x=(-22\pm 26)/(-32)`

`\\ \rm\rightarrowtail x=(-1)/(8)\:or\:(3)/(2)`

`\\ \rm\rightarrowtail x=-0.125\:or\:1.5`

#B

Vertex will be maximum

Coordinates are

• (0.688,10.563)

#C

• We have to find x intercepts (Part A)
• Then vertex(Part B)
• Then we can graph it

Answer 2

`\sf f(x) = -16x^2 + 22x + 3`

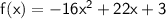
Part A

To find x-intercepts, the f(x) will be 0

`\sf \hookrightarrow -16x^2 + 22x + 3=0`

`\sf \hookrightarrow -16x^2 + 24x -2x+ 3=0`

`\sf \hookrightarrow -8x(2x-3)-1(2x- 3)=0`

`\sf \hookrightarrow (-8x-1)(2x+ 3)=0`

`\sf \hookrightarrow -8x-1=0 , \ 2x+ 3=0`

`\sf \hookrightarrow x=-0.125 , \ x=1.5`

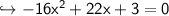
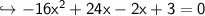
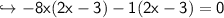
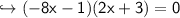
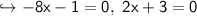
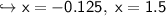
find y-intercept:

to find y-intercept, x will be 0

`\sf f(x) = -16(0)^2 + 22(0) + 3`

`\sf f(x) = 3`

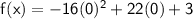
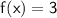
Part B

To find vertex use the formula: x = -b/2(a)

`\sf \rightarrow x = (-22)/(2(-16))`

`\sf \rightarrow x = 0.6875`

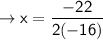
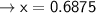
find y coordinates:

`\sf f(x) = -16(0.6875)^2 + 22(0.6875) + 3`

`\sf f(x) =10.5625`

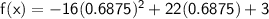
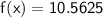
coordinates of vertex: (0.6875, 10.5625)

• 
  `\bold{\mathrm{If}\:a < 0,\:\mathrm{then\:the\:vertex\:is\:a\:maximum\:value}}`

• 
  `\bold{\mathrm{If}\:a > 0,\:\mathrm{then\:the\:vertex\:is\:a\:minimum\:value}}`

As its positive and greater than 0, the vertex will be Maximum.

part C

To draw the graph, simplify point the vertex on the graph. Then point both the x-intercepts. Also the y-intercept and draw the curve with free hand.

Graph attached: