Question

A 100-gallon fish tank fills at a rate of x gallons per minute. The tank has already been filling for 5 minutes. The function

f(x)-- - 5 represents the remaining time in minutes needed to fill the tank. How is the graph of the parent function (x)=
transformed to create the graph of the function fx) --
-5?

Answer 1

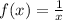C.) it is a vertical stretch with a factor of 100 and a translation 5 units down

Explanation:

Answer 2

- Stretching the parent function
`f(x) =(1)/(x)` vertically .

- Shifting the parent function
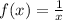`f(x) =(1)/(x)` 5 units right.

Explanation:

The complete exercise is: " A 100 gallon fish tank fills at a rate of x gallons per minute. The tank has already been filling for 5 minutes. The function
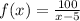`f(x) = (100)/(x -5)` represents the remaining time in minutes needed to fill the tank. How is the graph of the parent function
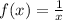`f(x) =(1)/(x)` transformed to create the graph of
`f(x) = (100)/(x -5)`?"

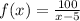Below are some transformations for a function :

1. If
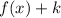`f(x)+k`, the function is shifted "k" units up.

2. If
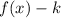`f(x)-k`, the function is shifted "k" units down.

3. If
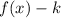`f(x)-k`, the function is shifted "k" units right.

4. If
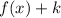`f(x)+k`, the function is shifted "k" units left.

5. If
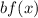`bf(x)` and
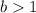`b>1` the function is stretched vertically by a factor of "b".

6. If
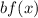`bf(x)` and
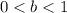`0<b<1` the function is compressed vertically by a factor of "b".

The exercise gives the following parent function:

`f(x) =(1)/(x)`

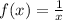
And you know that the transformed function which represents the remaining time in minutes needed to fill the tank, is:

`f(x) = (100)/(x -5)`

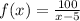
Therefore, based on the transformations explained before you can identify that the graph of the transformed function is created by:

- Stretching the parent function
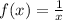`f(x) =(1)/(x)` vertically.

- Shifting the parent function
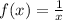`f(x) =(1)/(x)` 5 units right.