Answer:
The range of
 is
is
![f(x)\in[0,3]](https://img.qammunity.org/2023/formulas/mathematics/high-school/39e8b8trlepkxb4bdj7u4z31h6lfpqnzem.png)
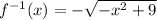 with a domain
with a domain
![x\in[0,3]](https://img.qammunity.org/2023/formulas/mathematics/high-school/lr7xllasjp49m8tniih4iq82t3klvbeym3.png)
Explanation:
Domain: set of input values (x-values)
Range: set of output values (y-values)
Given function:
![f(x)=√(9-x^2)\quad(x\in[-3,0])](https://img.qammunity.org/2023/formulas/mathematics/high-school/o5uy6wi08e7k11whlk1hunlegm724b68o8.png)
Therefore, as the original function has a restricted domain, its range is also restricted:

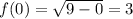
![\therefore\textsf{Range}\:f(x)\in[0,3]](https://img.qammunity.org/2023/formulas/mathematics/high-school/3bbzn5a0vx9d2zyug9aduws12dxbjkie46.png)
To determine the inverse of a function
Change
 to
to
 :
:
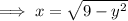
Square both sides:
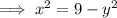
Switch sides:
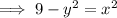
Subtract 9 from both sides:
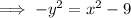
Divide both sides by -1:
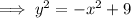
Therefore:
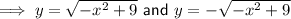
As the range of the inverse function is the same as the domain of the original function:
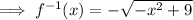 only as the range is [-3, 0]
only as the range is [-3, 0]
The domain of the inverse function is the same as the range of the original function.
![\therefore\textsf{Domain of}\:f^(-1)(x):x \in [0,3]](https://img.qammunity.org/2023/formulas/mathematics/high-school/q8b81beut2uftt5c4df6zt9xpv5ahbhhpk.png)
The inverse of a function is ordinarily the reflection of the original function in the line
 .
.
**Please see attached graph**