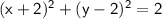1 Answer

Jeannot · Answer 1 · 2023-08-19T11:49:25+0000

Answer:

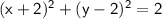
$\sf (x+2)^2+(y-2)^2=2$

Explanation:

If RS is the diameter of the circle, then the midpoint of RS will be the center of the circle.

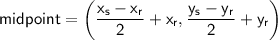
$\sf midpoint=\left((x_s-x_r)/(2)+x_r,(y_s-y_r)/(2)+y_r \right)$

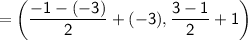
$\sf =\left((-1-(-3))/(2)+(-3),(3-1)/(2)+1 \right)$

$\sf =(-2, 2)$

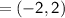
Equation of a circle:
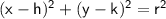
$\sf (x-h)^2+(y-k)^2=r^2$

(where (h, k) is the center and r is the radius)

Substituting found center (-2, 2) into the equation of a circle:

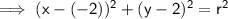
$\sf \implies (x-(-2))^2+(y-2)^2=r^2$

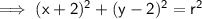
$\sf \implies (x+2)^2+(y-2)^2=r^2$

To find
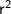$\sf r^2$ , simply substitute one of the points into the equation and solve:

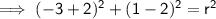
$\sf \implies (-3+2)^2+(1-2)^2=r^2$

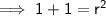
$\sf \implies 1+1=r^2$

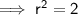
$\sf \implies r^2=2$

Therefore, the equation of the circle is:

$\sf (x+2)^2+(y-2)^2=2$

Please log in or register to add a comment.