Question

Kite WXYZ is graphed on a coordinate plane.

What is the approximate perimeter of the kite? Round to the nearest tenth.

10.6 units
11.5 units
14.0 units
16.2 units

Answer 1

16.2

Explanation:

Answer 2

Perimeter of the kite is 16.2 units rounding of to the nearest tenth.

Explanation:

Since, WXYZ is a kite, two separate pairs of repeated sides are congruent

This means,

WX=XY

WZ=ZY

∴, perimeter of kite WXYZ is = 2 (WX + WZ) Bar

(WX)Bar =
`\sqrt{(1-3){{2} \atop}\++(1+4){{2} \atop} } = \sqrt{(-2){{2} \atop}\++(-3){{2} \atop}} = √((4+9)) = √(13)`

(WZ)Bar =
`\sqrt{(1-3){{2} \atop}\++(1+3){{2} \atop} } = \sqrt{(-2){{2} \atop}\++(+4){{2} \atop}} = √((4+16)) = √(20)`

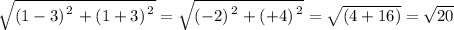
Hence, Perimeter P =
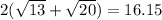`2(√(13) + √(20) ) = 16.15` ≈ 16.2 Units