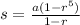Answer:
The value of s in the given equation is

Therefore
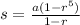
Explanation:
Given equation is
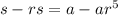
To find the value of s :
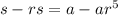
Taking common term "s" outside in LHS and common term "a" outside in RHS
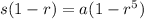
Dividing by (1-r) on both sides we get
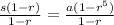
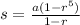
Therefore the value of s in the given equation is

Therefore