Question

If you invest $823 at an interest rate of 3% every 6 months, how much money will you have after 9 years

Answer 1

Explanation:

The compounding formula for this is

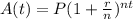`A(t)=P(1+(r)/(n))^(nt)` where A(t) is the amount after all the compounding is done, P is the initial investment, r is the interest rate as a decimal, n is the number of times the interest compounds per year, and t is the time in years. For us, our n is 2, since the money compounds every 6 months, and 6 months goes into 1 year 2 times. Our formula then is:

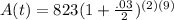`A(t)=823(1+(.03)/(2))^((2)(9))` which simplifies a bit to

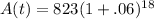`A(t)=823(1+.06)^(18)` which simplifies a bit more to

`A(t)=823(1.06)^(18)`

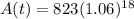
Raise 1.06 to the power of 18 and then multiply the 2 numbers together:

A(t) = 823(2.854339153) so

A(t) = 2349.12