
★ Given
- ➣A quadrilateral ABCD shape (kite) with diagonals "AC" and "BD"
- ➣ diagonal BD is of 8units
- ➣ diagonal AC is of 12units
✜ Now let's see about ques ✜
- question is asking about to find area of kite with the above info
- soo we know that
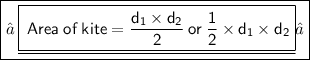

✜ Let's substitute value according to formula ✜
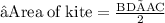


★Hence area of kite with diagonals BD = 8 units and AC = 12 units is


★ More info regarding this topic ★
- ➣ Quadrilateral:- A polygon with four sides,sum of it's interior angle is of 360⁰
- ➣ Kite is also a quadrilateral because of four sides.Kite is a quadrilateral which is proved Euclidean geometry.

Hope it helps !