Question

How do I do 10 and 11?

Answer 1

The value of b for question 10 is 10 and for question 11 is
`(1)/(3)`.

Explanation:

Step 1; We begin by identifying the various points along the curve. In this question, three points for both curves are given. So we have the values of x and f(x) from the points given. So to find the value if base b we have to substitute the values of x and f(x) in the equation.

Step 2; We substitute the values to find out the value of b and we check if b applies for the other values of the same curve again. For the curve in question 10, the given points along the curve are given as (-1,
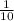`(1)/(10)`), (0,1), (1,10). so the values of x are -1, 0, 1 and different values of y are
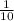`(1)/(10)`, 1, 10. When substituting values of x= 0, y= 1 it will satisfy the equation because any base with an exponential of 1 equals 1.

For (0,1), 1 =
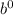`b^(0)`, 1=1

For (1, 10), 10 =
`b^(1)` so b =10

Now to check we substitute (-1,
`(1)/(10)`),
`(1)/(10)` =
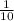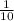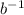`b^(-1)`, any base with a negative exponential means it is the reciprocal so

For (-1,
`(1)/(10)`),
`(1)/(10)` =
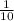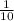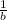`(1)/(b)`, b =10. So when checking we still get the same value of b.

Step 3; Now we substitute the values from the curve in question 11. The various values are (-1,3), (0,1) and (1,
`(1)/(3)`). By following the points given in the previous we solve these equations.

For (0,1), 1 =
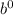`b^(0)`, 1=1

For (-1,3), 3 =
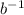`b^(-1)`, so 3 =
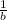`(1)/(b)`, b =
`(1)/(3)`

For (1,
`(1)/(3)`),
`(1)/(3)` =
`b^(1)`, b =
`(1)/(3)`.

So the values for b are 10 and
`(1)/(3)` for questions 10 and 11.