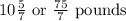Question

Help me on this question! Jake can carry 6 1/4 pounds of wood in from the barn.His father can carry 1 5/7 times as much as jake. How many pounds can Jake's farther carry?

Answer 1

Jake father can carry
`10(5)/(7) \text{ or } (75)/(7) \text{ pounds }`

Solution:

Given that,

Number of pounds Jake carry =
`6(1)/(4) \text{ pounds }`

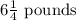
Number of pounds his father carry is
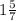`1(5)/(7)` times as much as jake

To find: Number of pounds Jake father can carry

Let us convert the mixed fractions to improper fractions

Multiply the whole number part by the fraction's denominator.

Add that to the numerator.

Then write the result on top of the denominator

`\rightarrow 6(1)/(4) = (4 * 6+1)/(4) = (25)/(4)\\\\\rightarrow 1(5)/(7) = (7 * 1+5)/(7) = (12)/(7)`

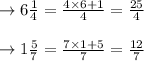
Then according to question,

`\text{Pounds father carry } = (12)/(7) \text{ times the pounds jake carry }\\\\\text{Pounds father carry } = (12)/(7) * (25)/(4)\\\\\text{Pounds father carry } = (75)/(7)\\\\\text{In terms of mixed fractions, }\\\\\text{Pounds father carry } = (75)/(7) = 10(5)/(7)`

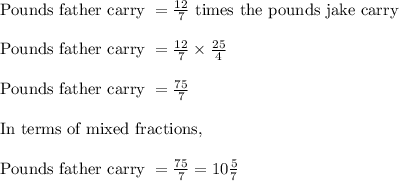
Thus Jake father can carry
`10(5)/(7) \text{ or } (75)/(7) \text{ pounds }`