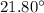Question

If the range of a projectile's trajectory is ten times larger than the height of the trajectory, then what was the angle of launch with respect to the horizontal? (Assume a flat and horizontal landscape.)

Answer 1

Angle of projection from the horizontal will be
`21.80^(\circ)`

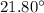
Step-by-step explanation:

We have given that range of the projectile is 10 times the height of the projectile

Let the projectile is projected with velocity u at an angle
`\Theta`

Range of the projectile is equal to
`R=(u^2sin2\Theta )/(g)`

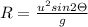
And height of the projectile is equal to
`h=(u^2sin^2\Theta )/(2g)`

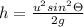
Now according to question range is 10 times of height

So
`(u^2sin2\Theta )/(g)=10* (u^2sin^2\Theta )/(2g)`

`sin2\Theta =5sin^2\Theta`

`2sin\Theta cos\Theta =5sin^2\Theta`

`tan\Theta =(2)/(5)=0.4`

`\Theta =tan^(-1)0.4=21.80^(\circ)`

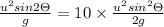
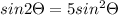
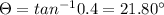
So angle of projection from the horizontal will be
`21.80^(\circ)`