Question

Within a school district, students were randomly assigned to one of two Math teachers - Mrs. Smith and Mrs. Jones. After the assignment, Mrs. Smith had 30 students, and Mrs. Jones had 25 students. (Hint: Here scores are coming from two different samples. We can compute variance from SD). At the end of the year, each class took the same standardized test. Mrs. Smith's students had an average test score of 78, with a standard deviation of 10; and Mrs. Jones' students had an average test score of 85, with a standard deviation of 15. Test the hypothesis that Mrs. Smith and Mrs. Jones are equally effective teachers. Use a 0.05 level of significance.

Answer 1

Answer: Yes we conclude that both teachers are effective.

Explanation:

Null Hypothesis,
`H_0` :
`\mu _1` =
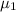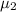`\mu _2` { It means both teachers are equally effective}

Alternate Hypothesis,
`H_1` :
`\mu _1` <
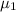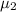`\mu _2` or

The test statistics here we use is :

`\frac{(X_1bar - X_2bar)-(\mu _1-\mu _2)}{s_p\sqrt{(1)/(n_1)+(1)/(n_2)}}` ~
`t_(_n_1 _+ _n_2 _-_2)`

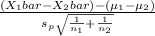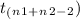
So now we will indicate each and every expression in the above test statistics,

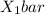`X_1bar` is the average test score of Mrs. smith's students = 78

`X_2bar` is the average test score of Mrs. Jones' students = 85

Formula for
`s_p` =
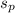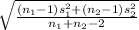`\sqrt{((n_1-1)s_1^(2)+(n_2-1)s_2^(2))/(n_1+n_2-2)}` ,where
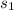`s_1` = 10 and
`s_2` = 15

`n_1` = 30 and
`n_2` = 25

putting values in
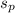`s_p`, we get

Now solving Test Statistics =
`\frac{(78-85)-0}{12.51414\sqrt{(1)/(30)+(1)/(25)}}` follows
`t_3_0_+_2_5_-_2`

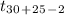
= -2.0656 follows
`t_5_3`

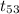
From the t table at 5% level of significance we know that our level of significance will lie between degree freedom 40 and 50 which is 1.684 to 1.671 and our test statistics is way more than this,

Hence we have do not have sufficient evidence to reject null hypothesis and we conclude that both teachers are equally effective.