Question

Let X be the mean of a random sample of size n = 64 from the uniform distribution on the interval (0, 3), i.e. f(x) = ( 1 3 , 0 < x < 3 0, otherwise.

1. Approximate the probability P(1.2 < X < 2.1).

Answer 1

P ( 1.2 < X < 2.1 ) = 0.3

Explanation:

Given:

Uniform distribution over interval (0,3) can be modeled by a probability density function f(x)

f(x) = 1 / (b - a)

Where a < x < b is the domain at which function is defined:

f(x) = 1 / (3) = 1 / 3

Where, X - U ( u , δ )

u = ( a + b ) / 2 = (0 +3) / 2 = 1.5

δ = ( b - a ) / sqrt (12) = (3 - 0) / sqrt (12) = 0.866

Hence,

X - U ( 1.5 , 0.866 )

There-fore calculating P ( 1.2 < X < 2.1 ):

`P ( 1.2 < X < 2.1 ) = \int\limits^b_a{f(x)} \, dx`

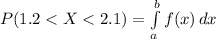
Where, a = 1.2 and b = 2.1

P ( 1.2 < X < 2.1 ) = x / 3 |

P ( 1.2 < X < 2.1 ) = 2.1 /3 - 1.2 / 3 = 0.3

Answer: P ( 1.2 < X < 2.1 ) = 0.3