Question

A skydiver jumps out of a hovering helicopter. A few seconds later, another diver jumps out, so they both fall along the same vertical line relative to the helicopter. Both divers fall with the same acceleration. Does the vertical distance between them a) increase, b) decrease or, c) stay the same? Does the difference in their velocities d)increase e) decrease or, f)stay the same? (the answer is (a) and (f) but how does the distance increase if their acceleration is the same?

Answer 1

The velocity of the first diver is always more than the velocity of the second diver hence more distance covered by the first diver over the same time

Step-by-step explanation:

In free fall

v^2 = u^2 + 2×g×S

If the initial velocity of the first diver = final velocity of the second diver then

v-u = constant

That means

S or distance between them is

= (v^2-u^2)/(2×g)

= (v+u)×(v-u)÷(2×g)

S = k×(v+u) where k = constant

Thus as v and u increases the distance between the two divers S increase

Answer 2

distance difference would a) increase

speed difference would f) stay the same

Step-by-step explanation:

Let t be the time the 2nd skydiver takes to travel, since the first skydiver jumped first, his time would be t + Δt where Δt represent the duration between the the first skydiver and the 2nd one. Remember that as t progress (increases), Δt remain constant.

Their equations of motion for distance and velocities are

`s_2 = gt^2/2`

`s_1 = g(t + \Delta t)^2/2`

`v_2 = gt`

`v_1 = g(t + \Delta t)`

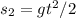
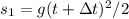
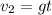
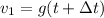
Their difference in distance are therefore:

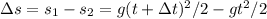
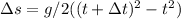
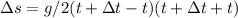`\Delta s = s_1 - s_2 = g(t + \Delta t)^2/2 - gt^2/2`

`\Delta s = g/2((t + \Delta t)^2 - t^2)`

`\Delta s = g/2(t + \Delta t - t)(t + \Delta t + t)` (As
`A^2 - B^2 = (A-B)(A+B)`

`\Delta s = g\Delta t/2(2t + \Delta t)`

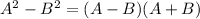
So as time progress t increases, Δs would also increases, their distance becomes wider with time.

Similarly for their velocity difference

`\Delta v = v_1 - v_2 = g(t + \Delta t) - gt`

`\Delta v = gt + g\Delta t - gt = g\Delta t`

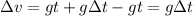
Since g and Δt both are constant, Δv would also remain constant, their difference in velocity remain the same.

This of this in this way: only the DIFFERENCE in speed stay the same, their own individual speed increases at same rate (due to same acceleration g). But the first skydiver is already at a faster speed (because he jumped first) when the 2nd one jumps. The 1st one would travel more distance compare to the 2nd one in a unit of time.