Answer:
a. -2x^2 + 3x+5=y
b.-x^2 +5x-4=y
c.-x^2 +6x-12=y
Explanation:
a.y=-2x^2 +bx+c
the points P and Q lie on curve
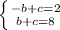
=> b=3, c=5
b. delta = b^2 +4c
x1=
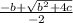 =4
=4
=>
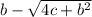 =8
=8
x2=
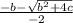 =1
=1
=>2=b+
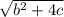
suppose :
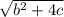 = a
= a
=>
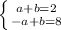
=> a=-3
b=5
a=-3 =>
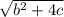 =-3 => b^2 +4c =9 =>5^2 +4c=9 => c=-4.
=-3 => b^2 +4c =9 =>5^2 +4c=9 => c=-4.
c.vertex (3;-3)
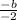 =3 => b =6
=3 => b =6
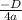 =
=
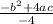 =-3 =>-b^2+4ac=12 => c=-12.
=-3 =>-b^2+4ac=12 => c=-12.