Question

juliet stands at the window of her apartment so that her eyes are 38.4 feet above the ground. juliet sees her boyfriend

Answer 1

13.67°

Explanation:

Here is the complete question: Juliet stands at the window of her apartment so that her eyes are 38.4 feet above the ground. Juliet sees her boyfriend down the street a few blocks away. She knows, based off the number of city block, that her boyfriend is at a distance of 156.45 feet away from the building. Determine the angle of depression of Juliet´s site to her boyfriend on the ground.

Given: Height of Juliet´s eye above ground is 38.4 ft.

Distance of Juliet´s boyfriend from the appartment´s base is 156.45ft.

Picture drawn to show case the condition in the question.

It form a right angle triangle, therefore we can use tangent rule to find angle of depression of Juliet´s site to her boyfriend on the ground.

We know,
`Tan\theta = (Opposite)/(adjacent)`

Where, adjacent= 156.45 ft

Opposite= 38.4 ft.

⇒
`Tan\theta= (38.4)/(156.45)`

⇒
`Tan\theta= 0.24544`

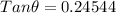
Now, using trignometry table to find value of arctan 0.24544

We will get,
`\theta= 13.79\º`

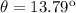
Hence, angle of depression is 13.79° of Juliet´s site to her boyfriend on the ground.