Question

A person has 8 friends, of whom 5 will be invited to a party:a) How many choices are there if 2 of the friends are feudingand will not attend together?b) how many choices if 2 of the friends will only attendtogether?

Answer 1

a) 36

b) 26

Explanation:

Data provided in the question:

Total friends = 8

Number of friends invited to the party = 5

Now,

a) if 2 of the friends are feuding will not attend together

= ( Total choices of selecting 5 friends out of 8 ) - (Choices in which both feuding will attend)

= ⁸C₅ - ⁶C₃

[ here, when both will come we will be left with inviting 3 friends out of 6 as 2 are already fixed. thus ⁶C₃ ]

=
`(8!)/(5!(8-5)!)-(6!)/(3!(6-3)!)`

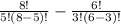
= 36

b) if 2 of the friends will only attend together

= Both attend the party + None of them attend the party

= ⁶C₃ + ⁶C₅

=
`(6!)/(3!(6-3)!)+(6!)/(5!(6-5)!)`

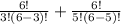
= 26