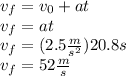Answer:
a.
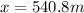
b.
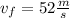
Step-by-step explanation:
a. David is moving with constant speed. While Tina is accelerating, we use the equations of uniformly accelerated motion.
For David we have:

For Tina:
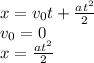
They both travel the same distance from the moment David passes her until she passes David:

Knowing this, we can calculate the distance:
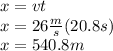
b. To calculate her speed when she passes him, we use: