Question

Recursive Formula. I need help!!!!!!!

Answer 1

h(1) = 2

h(n) = h(n – 1) + 12

Solution:

Given h(n) = –10 + 12n

To write the recursive formula of h(n), let us first find the sequence.

h(1) = –10 + 12(1) = 2

h(2) = –10 + 12(2) = 14

h(3) = –10 + 12(3) = 26

The sequence is 2, 14, 26, ....

So, the common difference of each term is 12.

Each term is 12 more than the previous term.

If
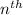`n^(th)` term is represented as
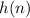`h(n)`, then the previous term is written as
`h(n-1)`.

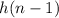h(n) = h(n – 1) + 12

Hence, the recursive formula of h(n) is

h(1) = 2

h(n) = h(n – 1) + 12