Question

What is the slope of the line containing the points (2/3,4) and (2,6)?

Answer 1

-7/8

Explanation:

What is the slope of the line containing the points (–2, 3) and (6, –4)?

Negative one-fourth

Negative one-half

Negative StartFraction 7 Over 8 EndFraction

Negative StartFraction 8 Over 7 EndFraction

Answer 2

The slope of the line containing the points (2/3, 4) and (2, 6) is
`(3)/(2)`

Solution:

Given that we have to find the slope of the line containing the points (2/3, 4) and (2, 6)

The slope of line is given by formula:

`m = (y_2-y_1)/(x_2-x_1)`

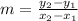
Here the given points are (2/3, 4) and (2, 6)

`(x_1, y_1) = ((2)/(3), 4)\\\\(x_2, y_2) = (2, 6)`

Substituting the values we get,

`m = (6-4)/(2-(2)/(3))\\\\m = (2)/((6-2)/(3))\\\\On\ simplifying\ we\ get,\\\\m = 2 * (3)/(4)\\\\m = (3)/(2)`

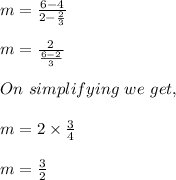
Thus slope of line is
`(3)/(2)`