Answer:
1) t=cubed rootinside d^2/va
2) v=at
3) a=sqrt vd/t^3
6) a=d/t^2
Explanation:
We are given the following:
In the SI unit system, time (t) is measured in seconds(s),
distance (d) is measured in meters(m)
velocity (v) is measured in meters per second
 , and
, and
acceleration (a) is measured in meters per second squared
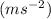 .
.
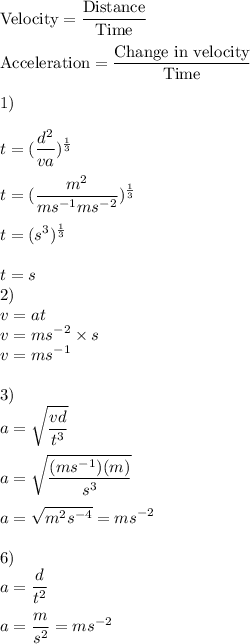
Thus, valid expressions are
1) t=cubed rootinside d^2/va
2) v=at
3) a=sqrt vd/t^3
6) a=d/t^2