Answer:
(a) 0.9412
(b) 0.9996 ≈ 1
Explanation:
Denote the events a follows:
 = a person passes the security system
= a person passes the security system
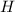 = a person is a security hazard
= a person is a security hazard
Given:

Then,
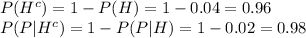
(a)
Compute the probability that a person passes the security system using the total probability rule as follows:
The total probability rule states that:
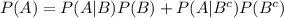
The value of P (P) is:
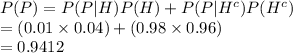
Thus, the probability that a person passes the security system is 0.9412.
(b)
Compute the probability that a person who passes through the system is without any security problems as follows:
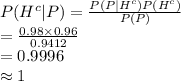
Thus, the probability that a person who passes through the system is without any security problems is approximately 1.