Question

You are camping with two friends, Joe and Karl. Since all three of you like your privacy, you don't pitch your tents close together. Joe's tent is 18.5 m from yours, in the direction 23.0 ∘ north of east. Karl's tent is 41.0 m from yours, in the direction 37.5 ∘ south of east.

Answer 1

35.7 m

Step-by-step explanation:

Let

`\mid A\mid=18.5 m`

`\mid B\mid=41 m`

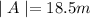
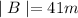
We have to find the distance between Joe's and Karl'e tent.

`A_x=Acos\theta`

`A_y=Asin\theta`

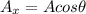
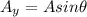
Substitute the values then we get

`A_x=18.5cos23^(\circ)=17 m`

`A_y=18.5sin 23^(\circ)=7.2 m`

`B_x=41cos37.5^(\circ)=32.5 m`

`B_y=41sin37.5^(\circ)=-24.96 m`

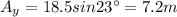
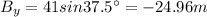
Because vertical component of B lie in IV quadrant and y-inIV quadrant is negative.

By triangle addition of vector

`B=A+C`

`C=B-A`

`C_x=B_x-A_x=32.5-17=15.5 m`

`C_y=B_y-A_y=-24.96-7.2=-32.16\approx=-32.2 m`

`\mid C\mid=√(C^2_x+C^2_y)`

`\mid C\mid=√((15.5)^2+(-32.2)^2)=35.7 m`

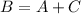
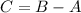
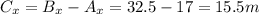
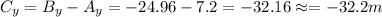
Hence, the distance between Joe's and Karl's tent=35.7 m