When comparing, the work
 done in stretching it from 30 cm to 40 cm (750k) with the work
done in stretching it from 30 cm to 40 cm (750k) with the work
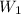 done in stretching the spring from 20 cm to 30 (500k) is 1.5 times.
done in stretching the spring from 20 cm to 30 (500k) is 1.5 times.
The work done on a spring is given by Hooke’s Law, which states that the force required to stretch or compress a spring by some distance (x) is proportional to that distance. That is, (F = kx), where (k) is the spring constant.
In addition, the work done on a spring is proportional to the square of the distance stretched, not the distance itself. So stretching the spring an additional 10 cm requires more work when the spring is already stretched.
The work done in stretching the spring is the integral of this force over the distance stretched, which gives us (W =
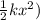 .
.
Let the work done in stretching the spring from 20 cm to 30 cm =
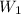
Let the work done in stretching the spring from 30 cm to 40 cm =

Then we have:
(
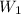
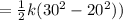
(
 =
=
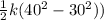
Solving these gives:
(
 = 500k)
= 500k)
(
 = 750k)
= 750k)
Thus, (
 = 1.5
= 1.5
 ) (750k/500k)
) (750k/500k)
Thus, the work done in stretching the spring from 30 cm to 40 cm is 1.5 times the work done in stretching it from 20 cm to 30 cm.