Question

A storage tank containing oil (SG=0.92) is 10.0 meters high and 16.0 meters in diameter. The tank is closed, but the amount of oil it contains can be determined from the gauge pressure at the bottom.A. A pressure gauge connected to the bottom of the tank was calibrated with the top of the tank open to the atmosphere. The calibration curve is a plot of height of oil,h(m), versus Pgauge (kPa). Sketch the expected shape of this plot. What height of oil would lead to a gauge reading of 68kPa? What would be the mass (kg) of oil in the tank corresponding to this height?B. An operator observes that the pressure gauge reading is 68kPa and notes the corresponding liquid height from the calibration curve. What he did not know was that the absolute pressure above the liquid surface in the tank was 115 kPa when he read the gauge. What is the actual height of the oil? (assuming atmsphereic pressure is 101 kPa)

Answer 1

a-1 Graph is attached. The relation is linear.

a-2 The corresponding height for 68 kPa Pressure is 7.54 m

a-3 The corresponding weight for 68 kPa Pressure is 1394726kg

b The original height of the column is 5.98 m

Step-by-step explanation:

Part a

a-1

The graph is attached with the solution. The relation is linear as indicated by the line.

a-2

By the equation

`P=\rho * g * h`

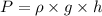
Here

• P is the pressure which is given as 68 kPa.
• ρ is the density of the oil whose SG is 0.92. It is calculated as

`\rho=S.G * \rho_(water)\\\rho=0.92 * 1000 kg/m^3\\\rho=920 kg/m^3\\`

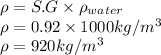
• g is the gravitational constant whose value is 9.8 m/s^2
• h is the height which is to be calculated

`P=\rho * g * h\\h=(P)/(\rho * g)\\h=(68 * 10^3)/(920 * 9.8)\\h=7.54m`

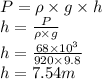
So the height of column is 7.54m

a-3

By the relation of volume and density

`M=\rho * V`

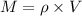
Here

• ρ is the density of the oil which is 920 kg/m^3
• V is the volume of cylinder with diameter 16m calculated as follows

`V=\pi r^2h\\V=3.14* (8)^2 * 7.54\\V=1515.23 m^3`

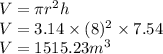
Mass is given as

`M=\rho * V\\M=920 * 1515.23\\M=1394726kg`

So the mass of oil leading to 68kPa is 1394726kg

Part b

Pressure variation is given as

`\Delta P=P_(obs)-P_(atm)\\\Delta P=115-101 kPa\\\Delta P=14 kPa\\`

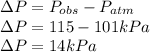
Now corrected pressure is as

`P_c=P_g-\Delta P\\P_c=68-14 kPa\\P_c=54 kPa`

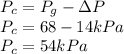
Finding the value of height for this corrected pressure as

`P_c=\rho * g * h\\h=(P_c)/(\rho * g)\\h=(54 * 10^3)/(920 * 9.8)\\h=5.98m`

The original height of column is 5.98m