We know that ABC is a triangle and if its a triangle every vertice conects to the other 2 vertices
So we can do the distance between AB, AC and BC then sum them
dAB =
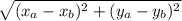
dAB =
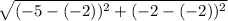
dAB =
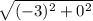
dAB = 3
dAC =
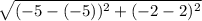
dAC =
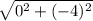
dAC = 4
dBC =
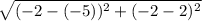
dBC =
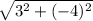
dBC =
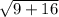
dBC =
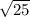
dBC = 5
3 + 4 + 5 = 12
So alternative A.