Step-by-step explanation:
The period of a mass-spring system is defined as:
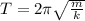
Here m is the block's mass and k is the spring constant
(a) We have
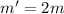 . So:
. So:
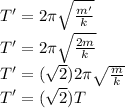
(b) We have
 . So:
. So:
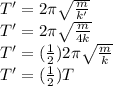
(c) The period does not depend on the oscillation amplitude, so we have the same period in both cases.