Step-by-step explanation:
Expression to calculate thermal resistance for iron (
 ) is as follows.
) is as follows.
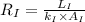
where,
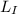 = length of the iron bar
= length of the iron bar
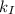 = thermal conductivity of iron
= thermal conductivity of iron
 = Area of cross-section for the iron bar
= Area of cross-section for the iron bar
Thermal resistance for copper (
 ) = \frac{L_{c}}{k_{c} \times A_{c}}[/tex]
) = \frac{L_{c}}{k_{c} \times A_{c}}[/tex]
where,
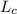 = length of copper bar
= length of copper bar
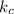 = thermal conductivity of copper
= thermal conductivity of copper
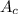 = Area of cross-section for the copper bar
= Area of cross-section for the copper bar
Now, expression for the transfer of heat per unit cell is as follows.
Q =
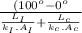
Putting the given values into the above formula as follows.
Q =

=

= 2.92 Joule
It is known that heat transfer per unit time is equal to the power conducted through the rod. Hence,
P =
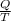
Here, T is 1 second so, power conducted is equal to heat transferred.
So, P = 2.92 watt
Thus, we can conclude that 2.92 watt power will be conducted through the rod when it reaches steady state.