Question

When you solve a system of equations algebraically, how can you tell whether the system has zero,one,or an infinite number of solutions?

Answer 1

By comparing the ratios of the coefficients, we can determine whether the system has zero,one,or an infinite number of solutions

Explanation:

Here, let us assume the given set of equations is:

`a_1x+b_1y+c_1 = 0\\a_2x+b_2y+c_2 = 0`

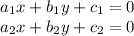
If the system is NOT in above form, convert it in such form.

Now, there are three cases of solution in the given system.

1. The system has NO or ZERO SOLUTION

Consider the given system.

If the ratio
`(a_1)/(a_2) = (b_1)/(b_2) \\eq(c_1)/(c_2)`

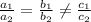
Then the given system of equations has NO SOLUTION.

2. The system has EXACTLY ONE SOLUTION

Consider the given system.

If the ratio
`(a_1)/(a_2) \\eq (b_1)/(b_2)`

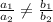
Then the given system of equations has UNIQUE SOLUTION.

3. The system has INFINITELY MANY SOLUTION

Consider the given system.

If the ratio
`(a_1)/(a_2) = (b_1)/(b_2) = (c_1)/(c_2)`

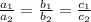
Then the given system of equations has INFINITELY MANY SOLUTION.