Answer:
0.613 meters is the smallest possible inside length of the tank.
Step-by-step explanation:
Length of the cubical steel tank =- l
Volume of the cube =
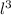
Volume of cubical steel tank =
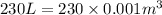
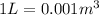
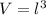
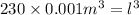
Solving of l :
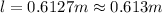
0.613 meters is the smallest possible inside length of the tank.