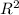Question

In Exercises 1–4, let S be the collection of vectors cxyd in R2that satisfy the given property. In each case, either prove thatS forms a subspace of R2 or give a counterexample to show that it does not.

Answer 1

S is not the subspace of
`R^2`

Explanation:

Let us suppose two vectors u and v belong to the S such that the property of xy≥0 is verified than

`u=\left[\begin{array}{c}-1 \\0\end{array}\right]`

`v=\left[\begin{array}{c}0 \\1\end{array}\right]`

Both the vectors satisfy the given condition as follows and belong to the S

`x_u y_u=-1* 0=0 \geq 0\\x_v y_v=1* 0=0 \geq 0\\`

Now S will be termed as subspace of R2 if

• u+v also satisfy the condition
• ku also satisfy the condition

Taking u+v

`u+v=\left[\begin{array}{c}-1 \\0\end{array}\right]+\left[\begin{array}{c}0 \\1\end{array}\right]\\u+v=\left[\begin{array}{c}-1+0 \\0+1\end{array}\right]\\u+v=\left[\begin{array}{c}-1 \\1\end{array}\right]`

Now the condition is tested as

`\\x_(u+v) y_(u+v)=-1* 1=-1 <0\\`

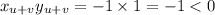
This indicates that the condition is not satisfied so S is not the subspace of
`R^2`