Question

The cone shaped roof has the height of 30ft and the radius of 15ft find it's lateral area and the surface area

Answer 1

• Lateral surface area of cone is 1580 feet²
• Surface area of cone is 2287 feet²

`\\`

Explanation:

Given that Height of cone shaped roof is 30 ft and radius is 15 ft.

To calculate the lateral surface area and Surface area of the cone we will use the formula given below:

`\\`

`\star \: { \underline { \boxed { \purple{ \pmb { \sf{Lateral \: surface \: Area _((cone)) = \pi rl}}}}}}`

`\\`

`\star{\underline{ \boxed{ \purple{ \pmb { \sf{Surface \: area _((cone)) = \pi rl + \pi {r}^(2) }}}}}}`

`\\`

Finding the Slant height of the cone:

`\dashrightarrow \: \:L = \sqrt{ {(r)}^(2) + {(h)}^(2) } \\`

`\dashrightarrow \: \: L = √(225 +900 ) \\`

`\dashrightarrow \: \: L = √(1125 ) \\`

`{ \dashrightarrow \: \: { \pink{ \boxed { \: L = 33.541 }}}}\\`

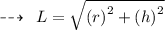
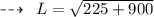
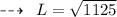
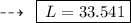
• Hence, Slant height of cone is 33.54 feet.

Substituting values in above formula:

`\dashrightarrow \: \: LSA = \pi rl \\`

`\dashrightarrow \: \: LSA = (22)/(7) * 15 * 33.54 \\`

`\dashrightarrow \: \: LSA = (22 * 15 * 33054)/(7) \\`

`\dashrightarrow \: \: LSA = (11068.2)/(7) \\`

`\dashrightarrow \: \:{ \boxed { \pmb{ \sf {\pink{ LSA \: \approx1580 \: {ft}^(2)}}} }} \\`

`\\`

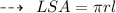
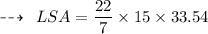
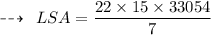
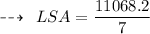
Hence, Lateral surface area of cone is 1580 feet²

Now, Calculating surface area:

`\dashrightarrow \: \:SA = \pi rl + \pi {r}^(2) \\`

`\dashrightarrow \: \:SA = \pi (15)(33.54) + \pi {(15)}^(2) \\`

`\dashrightarrow \: \:SA = \pi(503.1) + 22 5 \pi \\`

`\dashrightarrow \: \: SA = 728.1 \pi \\`

`\dashrightarrow \: \:SA = 728.1 * 3.14 \\`

`\dashrightarrow \: \:{ \boxed{ \pmb{ \pink{ \sf{SA \approx2287 \: {ft}^(2) }}}}}`

`\\`

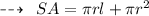
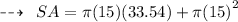
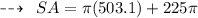
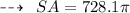
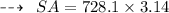
• Hence, surface area of cone is 2287 feet²