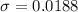Question

The following six independent length measurements were made (in feet) for a line: 736.352, 736.363, 736.375, 736.324, 736.358, and 736.383. Determine the most probable value.

Answer 1

a)
`\bar X =(736.352+736.363+736.375+736.324+736.358+736.383)/(6)=736.359`

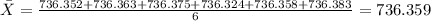
b) The sample deviation is calculated from the following formula:

`s=\sqrt{(\sum_(i=1)^n (X_i -\bar X)^2)/(n-1)}`

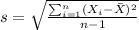
And for this case after replace the values and with the sample mean already calculated we got:

`s= 0.0206`

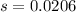
If we assume that the data represent a population then the standard deviation would be given by:

`\sigma=\sqrt{(\sum_(i=1)^n (X_i -\bar X)^2)/(n)}`

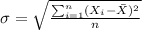
And then the deviation would be:

`\sigma=0.0188`

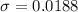
Explanation:

For this case we have the following dataset:

736.352, 736.363, 736.375, 736.324, 736.358, and 736.383

Part a: Determine the most probable value.

For this case the most probably value would be the sample mean given by this formula:

`\bar X =(\sum_(i=1)^n X_i)/(n)`

And if we replace we got:

`\bar X =(736.352+736.363+736.375+736.324+736.358+736.383)/(6)=736.359`

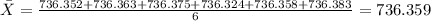
Part b: Determine the standard deviation

The sample deviation is calculated from the following formula:

`s=\sqrt{(\sum_(i=1)^n (X_i -\bar X)^2)/(n-1)}`

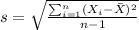
And for this case after replace the values and with the sample mean already calculated we got:

`s= 0.0206`

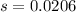
If we assume that the data represent a population then the standard deviation would be given by:

`\sigma=\sqrt{(\sum_(i=1)^n (X_i -\bar X)^2)/(n)}`

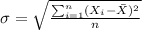
And then the deviation would be:

`\sigma=0.0188`