Find (a) the amplitude, (b) the wavelength, (c) the period, and (d) the speed of a wave whose displacement is given by y= 1.5 cos( 0.68 x+ 37 t), where x and y are in cm and t i…

Question

asked Sep 17, 2021 135k views

1 Answer

Eivindml · Answer 1 · 2021-09-20T13:10:44+0000

Answer with Step-by-step explanation:

We are given that displacement of wave

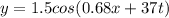
y=1.5cos(0.68x+37t)

Where y in cm and t in sec.

a.Compare it with

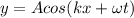
$y=Acos(kx+\omega t)$

Amplitude of wave=A

We get A=1.5

Amplitude=A=1.5 cm

b.k=0.68

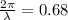
$(2\pi)/(\lambda)=0.68$

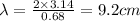
$\lambda=(2* 3.14)/(0.68)=9.2 cm$

Using
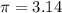
$\pi=3.14$

Wavelength of the wave=9.2 cm

c.Period=
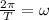
$(2\pi)/(T)=\omega$

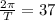
$(2\pi)/(T)=37$

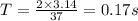
T=(2* 3.14)/(37)=0.17 s

The period of the wave=0.17 s

Speed of the wave=
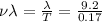
$\\u \lambda=(\lambda)/(T)=(9.2)/(0.17)$

Speed of the wave=54.1 cm/s