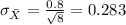Question

Calculate the standard deviation of the distribution of sample means. Write you answer in terms of fluid ounces and round to three decimal places. (Example: 0.398)

Answer 1

`\sigma_(\bar X) =(0.8)/(√(8))=0.283`

Explanation:

Assuming this question : "A bottling plant fills one-gallon jugs with milk. The labels on the jugs state that the volume of milk they contain is 128 fluid ounces (fl. oz.). Federal law mandates that the jugs must contain no less than the stated volume. The actual volume of milk in the jugs is normally distributed with mean μ=129 fl. oz. and standard deviation σ=0.8 fl. oz. Plant workers take a simple random sample (SRS) of 8 jugs, measure the volume of milk in each jug, and calculate the sample mean".

Previous concepts

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean".

Solution to the problem

Let X the random variable that represent the volume of milk in the jugs of a population, and for this case we know the distribution for X is given by:

`X \sim N(129,0.8)`

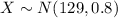
Where
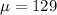`\mu=129` and
`\sigma=0.8`

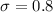
Since the distribution for X is normal then the distribution for the sample mean is given by:

`\bar X \sim N(\mu, (\sigma)/(√(n)))`

And the standard deviation for the sample mean would be given by:

`\sigma_(\bar X) =(0.8)/(√(8))=0.283`