Answer:
The range of the measure of third side is
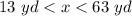 .
.
Explanation:
Given:
measure of the first side = 25 yd
measure of the second side = 38 yd
We need to find the range for the measure of the third side.
Solution:
Let the measure of the third side be 'x'.
Now by Triangle Inequality property which states.
Measure of the third side must be less than the sum of the measures of other two side and greater than difference of the measures of other two side.
Sum of two sides = measure of the first side + measure of the second side =
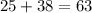
Difference of two sides = measure of the second side - measure of the first side =
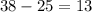
framing the above quote in equation form we get;
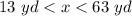
Hence the range of the measure of third side is
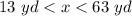 .
.