Question

Consider an ideal gas at 27.0 degrees Celsius and 1.00 atmosphere pressure. Imagine the molecules to be uniformly spaced, with each molecule at the center of a small cube. What is the length of an edge of each small cube if adjacent cubes touch but don't overlap?

Answer 1

The length of an edge of each small cube is 3.43 nm.

Step-by-step explanation:

Given that,

Temperature of ideal gas =27.0°C

Pressure = 1.00 atm

We need to calculate the length of an edge of each small cube

Using gas equation

`PV=nRT`

`PV=NkT`

`V=(NkT)/(P)`

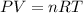
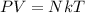
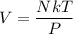
For, N = 1

Where,

N = number of molecule

k = Boltzmann constant

T = temperature

P= pressure

Put the value into the formula

`V=(1*1.38*10^(-23)*(27+273))/(1.03*10^(5))`

`V=4.019*10^(-26)\ m^3`

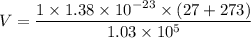
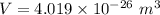
Now, for the cube

`V=L^3`

`L=V^{(1)/(3)}`

`L=(4.019*10^(-26))^{(1)/(3)}`

`L=3.43*10^(-9)\ m`

`L=3.43 nm`

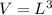
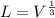
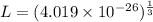
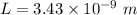
Hence, The length of an edge of each small cube is 3.43 nm.