Question

The radius of the circle traced out by the second hand on a clock is 6.00 cm. In a time t the tip of the second hand moves through an arc length of 19.0 cm. Determine the value of t in seconds.

Answer 1

30.29 s

Step-by-step explanation:

We are given that

Radius=r=6 cm

Length of an arc=l=19 cm

We have to find the value of t in seconds.

`\theta=(l)/(r)`

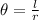
Substitute the values then we get

`\theta=(19)/(6)=3.17 rad`

We know that

1 minute=60 seconds

In 60 seconds ,second hand makes an angle=
`2\pi`radian

`2\pi` radian made by second had in 60 sec.

1 radian made by second hand in
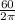`(60)/(2\pi)` sec

3.17 rad made by second hand in
`(60)/(2\pi)* 3.17=(60)/(2* 3.14)* 3.17=30.29 s`

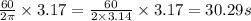
Hence, the value of t =30.29 s