Answer:

Explanation:
Given differential equation,
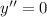
Characteristic equation is given by
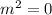
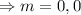 .
.
Differential equation have repeated roots and solution of differential equation is
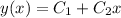 .............................(1)
.............................(1)
Initial conditions are
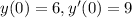
Plugging first condition in equation (1),
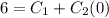
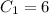
Equation (1) becomes
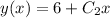 ............................(2)
............................(2)
differentiate equation (2) with respect to 'x',
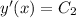
Plugging second condition,
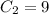
Hence,
