Question

A 27.0-m steel wire and a 48.0-m copper wire are attached end to end and stretched to a tension of 145 N. Both wires have a radius of 0.450 mm, and the densities are 7.86 × 103 kg/m3 for the steel and 8.92 × 103 kg/m3 for the copper. (Note that these are mass densities, mass per unit volume, not linear mass densities, mass per unit length.)How long does a wave take to travel from one end to the other end of the combination wire?

Answer 1

The time taken by the wave to travel along the combination of two wires is 458 ms.

Step-by-step explanation:

Given that,

Length of steel wire= 27.0 m

Length of copper wire = 48.0 m

Tension = 145 N

Radius of both wires = 0.450 mm

Density of steel wire
`\rho_(s)= 7.86*10^(3)\ kg/m^(3)`

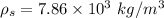
Density of copper wire
`\rho_(c)=8.92*10^(3)\ kg/m^3`

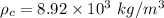
We need to calculate the linear density of steel wire

Using formula of linear density

`\mu_(s)=\rho_(s)A`

`\mu_(s)=\rho_(s)*\pi r^2`

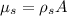
Put the value into the formula

`\mu_(s)=7.86*10^(3)*\pi*(0.450*10^(-3))^2`

`\mu_(s)=5.00*10^(-3)\ kg/m`

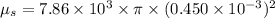
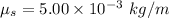
We need to calculate the linear density of copper wire

Using formula of linear density

`\mu_(c)=\rho_(s)A`

`\mu_(c)=\rho_(s)*\pi r^2`

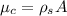
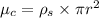
Put the value into the formula

`\mu_(c)=8.92*10^(3)*\pi*(0.450*10^(-3))^2`

`\mu_(c)=5.67*10^(-3)\ kg/m`

We need to calculate the velocity of the wave along the steel wire

Using formula of velocity

`v_(s)=\sqrt{(T)/(\mu_(s))}`

`v_(s)=\sqrt{(145)/(5.00*10^(-3))}`

`v_(s)=170.3\ m/s`

We need to calculate the velocity of the wave along the steel wire

Using formula of velocity

`v_(c)=\sqrt{(T)/(\mu_(c))}`

`v_(c)=\sqrt{(145)/(5.67*10^(-3))}`

`v_(c)=159.9\ m/s`

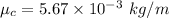
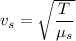
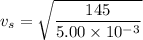
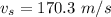
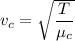
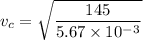
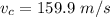
We need to calculate the time taken by the wave to travel along the combination of two wires

`t=t_(s)+t_(c)`

`t=(l_(s))/(v_(s))+(l_(c))/(v_(c))`

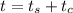
Put the value into the formula

`t=(27.0)/(170.3)+(48.0)/(159.9)`

`t=0.458\ sec`

`t=458\ ms`

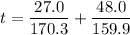
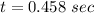
Hence, The time taken by the wave to travel along the combination of two wires is 458 ms.