Question

The sides of a right triangle measure 6 times the square root of 3, 6 inches, and 12 inches. If an altitude is drawn from the right angle to the hypotenuse, what is the length of the segment of the hypotenuse adjacent to the shorter leg? What is the length of the alitude?

Answer 1

Length of segment of the hypotenuse adjacent to the shorter leg is 5 inches and the length of the altitude is 3 inches.

Explanation:

Step 1: Let the triangle be ΔABC with right angle at B. The altitude drawn from B intersects the hypotenuse AC at D. So 2 new right angled triangles are formed, ΔADB and ΔCDB.

Step 2: According to a theorem in similarity of triangles, when an altitude is drawn from any angle to the hypotenuse of a right triangle, the 2 newly formed triangles are similar to each other as well as to the bigger right triangle. So ΔABC ~ ΔADB ~ ΔCDB.

Step 3: Identify the corresponding sides and form an equation based on proportion. Let the length of the altitude be x. Considering ΔABC and ΔADB, AB/DB = AC/AB

⇒ 6/x = 12/6

⇒ 6/x = 2

⇒ x = 3 inches

Step 4: To find length of the hypotenuse adjacent to the shorter leg (side AB of 6 inches), consider ΔADB.

⇒
`AD^(2) + BD^(2) = AB^(2)`

⇒
`AD^(2) =AB^(2) - BD^(2)`

⇒
`AD^(2) =6^(2) -3^(2)`

⇒
`AD^(2) =36 - 9 = 25`

⇒
`AD = √(25)`

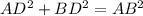
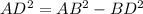
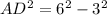
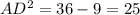
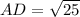
⇒AD = 5 inches