Answer: a. 0.14085
b. 3.826 x

c. 0.5437
d. 0.0811
Explanation:
Given average amount parents and children spent per child on back-to-school clothes in Autumn 2010 ,
 = $527
= $527
Given standard deviation ,
 = $160
= $160
Let X = amount spent on a randomly selected child
Also Z =

a. Probability(X>$700) = P(
 >
>
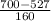 ) = P(Z>1.08125) = 0.14085 {Using Z % table}
) = P(Z>1.08125) = 0.14085 {Using Z % table}
b. P(X<100) = P( Z <
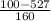 ) = P(Z< -2.66875) = P(Z > 2.66875) = 3.826 x
) = P(Z< -2.66875) = P(Z > 2.66875) = 3.826 x

c. P(450<X<700) = P(X<700) - P(X<=450)
P(X<700) = 1 - P(X>=700) = 1 - 0.14085 = 0.8592
P(X<=450) = P(Z<=
 ) = P(Z<= -0.48125) = P(Z<=0.48125) = 0.3155
) = P(Z<= -0.48125) = P(Z<=0.48125) = 0.3155
So final P(450<X<700) = 0.8592 - 0.3155 = 0.5437
d. P(X<=300) = P(Z<=
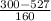 ) = P(Z<= -1.4188) = P(Z>=1.4188) = 0.0811
) = P(Z<= -1.4188) = P(Z>=1.4188) = 0.0811
All the above probabilities are calculated using Z % table along with interpolation between two values.