Question

A gasoline engine takes in air at 290 K, 90 kPa and then compresses it. The combustion adds 1000 kJ/kg to the air after which the temperature is 2050 K. Using a cold airstandard analysis, i.e., constant specific heats at 300 K, find the compression ratio, compression specific work, and the highest pressure in the cycle.

Answer 1

4883 kPa

Step-by-step explanation:

Standard Otto Cycle pics are attached

Combustion process:

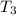`T_(3)` = 2050 K

`U_(2)` =
`U_(3)` -
`Q_(h)`

`T_(2)` =
`T_(3)` -
`Q_(h)` /
`C_(vo)`

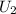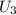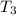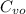
= 2050 - 1000 / 0.717

= 655.3 K

Compression process:

`P_(2)` =
`P_(1)` (
`T_(2)` /
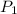`T_(1)`)^k/(k-1)

= 90(655.3/290) ^3.5

= 1561 kPa

CR = v1 / v2 = (
`T_(2)` /
`T_(1)`))^1/(k-1)

= (655.3 / 290) ^2.5

= 7.67

w2 = u2 - u1 =
`C_(vo)`(
`T_(2)` -
`T_(1)`)

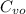= 0.717(655.3 - 290)

= 262 kJ / kg

Highest pressure is after the combustion

`P_(3)` =
`P_(2)`
`T_(3)` /
`T_(2)`

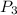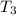= 1561 × 2050 / 655.3

= 4883 kPa