Question

Graph y > -1/3x+5

`y > - (1)/( 3 ) x + 5`
​

Answer 1

Step-by-step explanation:

The function is
`y>-(1)/(3) x+5`

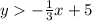
To graph the function, let us find the x and y intercepts.

To find x-intercept, let us substitute y=0 in the function
`y>-(1)/(3) x+5`

`\begin{aligned}0 &=-(1)/(3) x+5 \\-5 &=-(1)/(3) x \\x &=15\end{aligned}`

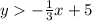
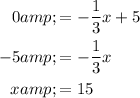
Thus, the x-intercept is
`(15,0)`

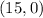
To find the y-intercept, let us substitute x=0, we get,

`\begin{aligned}&y=-(1)/(3)(0)+5\\&y=5\end{aligned}`

Thus, the y-intercept is
`(0,5)`

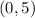
The graph has no asymptotes.

To plot the points in the graph, we need to substitute the values for x in the function
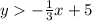`y>-(1)/(3) x+5`, to find the y-values.

The points are
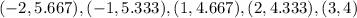`(-2,5.667),(-1,5.333),(1,4.667),(2,4.333),(3,4)`. The image of the graph and table is attached below: