Answer:
a.
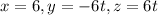
b.
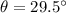
Explanation:
We are given that
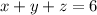

a.Substitute z=0
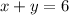 ...(1)
...(1)
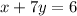 ..(2)
..(2)
Subtract equation (1) from equation (2)
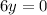
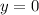
Substitute y=0 in equation(1)
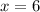
The point (6,0,0) lie on a line.
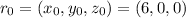
Let
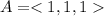
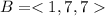
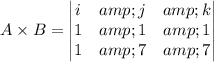
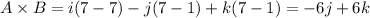
Therefore, the vector
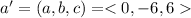
Line is parallel to vector a' and passing through the point (6,0,0).
The parametric equation is given by
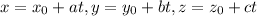
Using the formula
The parametric equation is given by
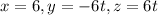
Angle between two plane
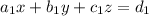
and
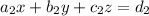
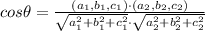
Using the formula
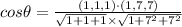
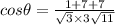
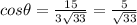
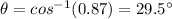
Where
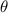 in degree.
in degree.