Question

Find the missing lengths. If needed, round the answers to the nearest tenth.

Answer 1

The value of y is 64.

The value of z is 225.

Explanation:

Given,

AB = 136

BC = 255

∠B = 90°

We have to find the value of 'y' and 'z'.

Solution,

Let assume D is a point on AC.

Then BD = 120

And also given ∠D = 90°

Now in ΔABD

AB = 136 and BD = 120

∠D = 90°

So according to Pythagoras theorem;

"The square of the hypotenuse is equal to the sum of the squares of the other two sides".

`AB^2=BD^2+AD^2`

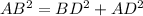
On substituting the values, we get;

`136^2=120^2+y^2\\\\18496=14400+y^2\\\\y^2=18496-14400\\\\y^2=4096`

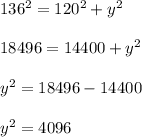
Now taking square root on both side, we get;

`√(y^2) =√(4096) \\\\y=64`

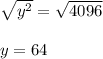
Hence the value of y is 64.

Again, in ΔBDC

BC = 255 and BD = 120

∠D = 90°

So according to Pythagoras theorem;

"The square of the hypotenuse is equal to the sum of the squares of the other two sides".

`BC^2=BD^2+DC^2`

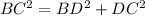
On substituting the values, we get;

`255^2=120^2+z^2\\\\65025=14400+z^2\\\\z^2=65025-14400\\\\z^2=50625`

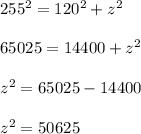
Now taking square root on both side, we get;

`√(z^2)=√(50625)\\\\z=225`

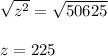
Hence the value of z is 225.